A média geométrica é um mecanismo utilizado matematicamente para representar situações em que ocorrem aumentos sucessivos em um mesmo conjunto. Em outras palavras, é um conceito estatístico bastante utilizado na matemática financeira.
Ele é utilizado, entre outras funções, para comparar prismas e cubos que tenham o mesmo volume, além de quadrados e retângulos com áreas iguais. Ademais, também pode ser aplicado em situações de acúmulo da taxa percentual, isto é, situações de porcentagem sob porcentagem.
Fórmula para o cálculo da média geométrica
O cálculo da média geométrica é para encontrar a raiz enésima obtida a partir do produto dos elementos. Ela é utilizada para definir o valor médio de uma série de dados sucessivos. Por exemplo, para encontrar entre 2, 3, 4 e 7, é preciso multiplicar os quatro valores e, em seguida, tirar a raiz quarta do resultado obtido inicialmente. Veja abaixo:
Mg = √42 · 3 · 4 · 7
Mg = √4168 Mg ≈ 3,6
O primeiro passo é contar a quantidade de termos presentes no problema, para eleger qual raiz será tirada. Dessa forma, tirar a média geométrica com cinco elementos, por exemplo, é eleger, ao fim, a raiz quinta do valor obtido a partir da multiplicação entre os valores.
Uma outra aplicação pode ser solicitada em uma situação de comparação entre polígonos, como na imagem abaixo. Qual seria o valor x dos lados do quadrado?
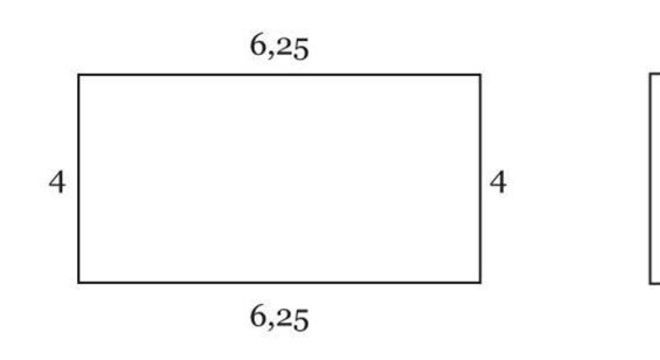
Nessa situação, utilizaríamos a média geométrica. Como resultado, a área do retângulo seria a raiz quadrada da multiplicação entre 4 · 6,25.
Mg = √ 25
Mg = 5
Desse modo, o lado do quadrado mediria 5.
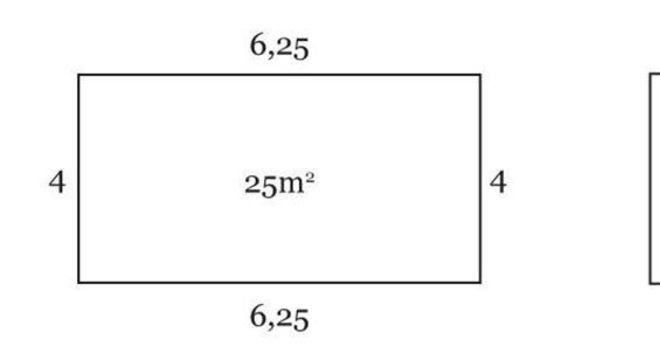
Esse é o método mais comum, utilizado geralmente quando temos alguma calculadora por perto.
Em contrapartida, o outro método que pode ser utilizado é o da fatoração.
Método da fatoração
O segundo método da média geométrica permite tirar a fatoração de cada valor a fim de facilitar o cálculo.
Assim, para encontrar a média geométrica de {3,25,27}, podemos:
3 = 3 25 = 5² 27 = 3³
Mg = √4 3 · 5² · 3³ Mg = √4 34 · 5² Mg = 3 · √4 25 Mg = 3 · 2,23 Mg ≈ 6,69
Em seguida, um outro exemplo a ser aplicado envolve porcentagens. Um determinado produto, ao longo de quatro meses, possuiu vários aumentos consecutivos de 25%, 15%, 10% e 20%, respectivamente. Qual a média desses aumentos ao final do quarto mês?

Uma vantagem dos cálculos proporcionais é a possibilidade do valor ser transformado em formas decimais, o que facilita a simplificação dos cálculos. Sendo assim, podemos utilizar o seguinte raciocínio: o valor total do produto, antes dos aumentos, correspondia a 100%. Se no primeiro mês ele cresceu 25%, logo temos 125% ou 1,25.
Seguindo essa lógica, os outros três aumentos foram de 115% (1,15), 110% (1,1) e 120% (1,2). Portanto, podemos tirar a raiz enésima (quarta) do produto entre os valores decimais:
Mg = √4 1,25 · 1,15 · 1,1 · 1,2
Mg = √4 1,8975 Mg ≈ 1,173
Média geométrica e média aritmética
Para o cálculo de dados estatísticos, é importante saber qual tipo de média pode ser utilizada para a obtenção de valores centrais.

Dessa forma, a média geométrica deve ser utilizada quando os dados estão em progressão geométrica, isto é, de maneira sucessiva e com dados sem definições exatas.
Por outro lado, a média aritmética pode ser utilizada nos demais casos, isto é, sem que os dados estejam colocados de maneira crescente. Por exemplo, para calcular a média de notas escolares entre quatro irmãos (7,8; 8,5; 6,9 e 9,2) podemos somar as quatro medidas e dividir o valor final por quatro. O resultado médio seria, então, 8,1.
MAS = 7,8 · 8,5 · 6,9 · 9,2 / 4
MAS = 8,1
Essa é a média aritmética do tipo simples, ou seja, que não possui repetição de dados.
Média aritmética ponderada
Ao contrário dela, a média aritmética ponderada apresenta essa repetição e os cálculos também variam.
Digamos que entre os quatro maiores artilheiros de um campeonato de futebol, o saldo tenha sido de 17 gols entre os dois primeiros colocados, 14 gols do terceiro colocado e 11 gols do quarto e do quinto. Como resultado, qual seria a média aritmética de gols nesse campeonato?

Como há repetição de valores, os elementos que se repetem (x1) devem ser multiplicados pela quantidade de vezes que se repetem (k1), o que deve ser feito entre todas repetições, e somados. Em seguida, o resultado deve ser dividido pela quantidade total de repetições.
MAP = (17 · 2) + 14 + (11 · 2) / 2 + 2
MAP = 34 + 14 + 22 / 4 MAP = 17,5
Portanto, a média de gols entre os artilheiros do campeonato foi de 17,5 gols.
Então, esperamos que você tenha aprendido sobre como calcular uma média geométrica e quando utilizá-la. Se gostou da matéria, confira também o que é média aritmética.
Fontes: Mundo Educação, Brasil Escola, Toda Matéria
Imagens: Educa Mais Brasil, COC, Rádio Hertz,Pense Vestibular. Mercado e Consumo.
Essa matéria Média Geométrica – O que é, fórmula e exemplos de aplicação foi criada pelo site Conhecimento Científico.
